ملخص وحدة الغازات كيمياء عاشر متقدم

ملخص وحدة الغازات كيمياء عاشر متقدم

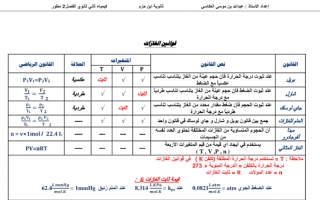
قوانين الغازات

القانون / نص القانون 

بويل عند ثبوت درجة الحرارة فأن حجم عينة من الغاز يتناسب تناسب عكسيا مع الضغط 

شارل عند ثبوت الضغط فأن حجم عينة من الغاز يتناسب تناسب طردية مع درجة الحرارة 

جاي لوسك عند ثبوت الحجم فأن ضغط مقدار محدد من الغاز يتناسب تناسب طرديا مع درجة الحرارة 

العام للغازات جمع بين قانون بویل و شارل و جاي لوساك في قانون واحد

مبدأ أفوجادرو أن الحجوم المتساوية من الغازات المختلفة تحتوي العدد نفسه من الجسيمات

الغاز المثالي يستخدم في أيجاد أي قيمة من قيم المتغيرات الأربعة  

ملاحظة :

T = تستخدم درجة الحرارة المطلقة (كلفن K) في قوانين الغازات 

درجة الحرارة بالكلفن = الدرجة المئوية + 273 

n = عدد المولات R = ثابت الغازات

( 7 - 1 ) قوانين الغازات The Gas Laws

الفكرة الرئيسة : إذا تغير ضغط أي كمية ثابتة من غاز أو درجة حرارتها أو حجمها فيتأثر المتغيرين الآخرين . 

قانون بویل :  ضغط الغاز و حجمه مترابطان .وقد وصف العالم روبرت بويل هذه العلاقة .

قانون بويل حجم مقدار محدد من الغاز يتناسب عكسيا مع الضغط الواقع علية عند ثبوت درجة الحرارة 

العلاقة عكسية بين حجم الغاز و الضغط الواقع عليه

P P1V1 = p2V2  : تمثل الضغط ,V : تمثل الحجم 

القانون الرياضي حاصل ضرب ضغط كمية محددة من الغاز في حجمها عند ثبوت درجة حرارتها يساوي كمية ثابتة

يمثل كل من P و v الضغط و الحجم الابتدائيين و P و ,v الضغط و الحجم الجديدين . 

مثال : قانون بويل ينفخ غواص وهو على عمق 10 تحت الماء فقاعة هواء حجمها L 0 .75، وعندما ارتفعت فقاعة الهواء إلى السطح تغير ضغطها من atm 2 . 25 إلى atm 1 .03 ، ما حجم فقاعة الهواء عند السطح 

تحليل المسألة بالاعتماد على قانون بویل، بنقصان الضغط على فقاعة الهواء يزداد حجمها، لذا يجب ضرب الحجم الابتدائي لها في نسبة ضغط أكبر من 1. 

المطلوب? L, V2

المعطيات V1 = 0.75L P = 2.25 atm P2 = 1.03 atm

حساب المطلوب استخدم قانون بویل لإيجاد قيمة V واحسب الحجم الجديد. 

ضع نص قانون بويل

اضرب الأرقام والوحدات و اقسمها

قانون شارل : - درس جاك شارل العلاقة بين الحجم و درجة الحرارة . حيث لاحظ أن كلا من درجة الحرارة و حجم عينة من الغاز يزداد عندما يبقى كل من مقدار العينة و الضغط ثابتين

- يمكن تفسير هذه الخاصية بناء على نظرية الحركة الجزيئية : فعندما تزداد درجة الحرارة تتحرك جسيمات الغاز و اتصطدم أسرع بجدار الإناء الذي توجد فيه و بقوة أكبر . 

- الضغط يعتمد على عدد و قوة اصطدامات جسيمات الغاز بجدار الإناء فإن هذا يؤدي إلى زيادة الضغط . 

- حتى يبقى الضغط ثابتا لا بد أن يزيد الحجم إذ تحتاج الجسيمات إلى الانتقال إلى مسافات أبعد قبل أن تصطدم بالجدار مما يقلل من عدد اصطدامات الجسيمات بجدار الإناء. ( أنظر شكل 2 - 7) 

رسم العلاقة بين درجة الحرارة و الحجم منحني درجة الحرارة مع الحجم خط مستقيم ( أنظر شكل 2 - 7) 

درجة الصفر المطلق هو يمثل أقل قيمة ممكنة لدرجة الحرارة ( بلكلفن) التي تكون عندها طاقة الذرات أقل ما يمكن 

قانون شارل حجم مقدار محدد من الغاز يتناسب طرديا مع درجة الحرارة المطلقة عند ثبوت الضغط . 

العلاقة علاقة طردية بين الحجم و درجة الحرارة

القانون الرياضي تمثل T1 و ۷1 درجة الحرارة والحجم الابتدائي T2 و V2 درجة الحرارة والحجم الجديدين 

ملاحظة عند استخدام قانون شارل يعبر عن درجة الحرارة بالكلفن ( مطلقة ) 

الشكل 2 - 7 عند تسخين الأسطوانة تزداد الطاقة الحركية لجسيمات الغاز، فتدفع الجسيمات المكبس إلى أعلى. يوضح الرسم البياني الآتي علاقة الحجم بدرجة الحرارة السيليزية ودرجة الحرارة المطلقة.

قانون تحويل درجة الحرارة من المئوية إلى الكلفن

درجة الحرارة بالمئوية ( سيليزية ): ,T 

قانون شارل إذا كان حجم بالون هيليوم 2.32 L داخل سيارة مغلقة، عند درجة حرارةC" 40.0 ، فإذا وقفت السيارة في ساحة البيت في يوم حار وارتفعت درجة الحرارة داخلها إلى 75.0°C ، فما الحجم الجديد للبالون إذا بقي الضغط ثابتا ؟ 

تحليل المسألة ينص قانون شارل على أن حجم مقدار محدد من الغاز يزداد بزيادة درجة حرارته إذا بقي الضغط ثابتا. لذا يزداد حجم البالون ، ويجب ضرب الحجم الابتدائي في نسبة درجة حرارة أكبر من واحد. 

المطلوب = ? L، V2

المعطيات T2 = 40.0°C  = 2.32L V T2 = 75.0°C

حساب المطلوب حول درجة الحرارة السيليزية إلى الكلفن. استخدم معامل التحويل عوض بقيمة T

T = 273 + 40.0°C = 313.0K

T2 = 273 + 75.0°C = 348.0K

عوض بالقيم المعروفة في المعادلة التي أعيد ترتيبها.

ملاحظة : يستخدم معامل التحويل L/ mol 22.4 فقط في الظروف المعيارية 

قانون الغاز المثالي - الكتلة المولية و الكثافة

يمكن استخدام قانون الغاز المثالي في أيجاد أي قيمة من قيم المتغيرات الأربعة :( T , V , P , n ) . كما يمكن حساب الكتلة المولية و الكثافة لعينة غاز

حيث : الكتلة بالجرام = m الكتلة المولية = M كثافة المادة = D 

- لماذا نحتاج إلى معرفة كثافة الغاز ؟

تستخدم الطفاية المحتوية على غاز co2 لإطفاء الحريق بسبب أن كثافة غاز co2 أكبر من كثافة الهواء فيحل غاز co2 محل غاز O2 فيتم عزل الهواء عن الحريق . 

الغاز الحقيقي مقابل الغاز المثالي :

خصائص الغازات المثالية 

1 تتبع فرضيات نظرية الحركة الجزيئية

2 حجم جسيمات الغاز المثالي يكاد يكون معدوما . 

3 لا تشغل حيزا . 

4 لا توجد قوی تجاذب بينها و لا تتجاذب مع جدران الوعاء ولا تتنافر معه . 

5 تتحرك جسيمات الغاز المثالي حركة عشوائية دائمة في خطوط مستقيمة . 

6 يتبع الغاز المثالي قوانين الغازات تحت كل الظروف من ضغط و درجة حرارة 

7 تصادم الجسيمات في الغازات المثالية مرنة .

- لكن في الحقيقة ليس هناك غاز مثالي .

- متى يكون قانون الغاز المثالي غير مناسب للاستخدام مع الغاز الحقيقي ؟ 

- تحيد معظم الغازات الحقيقية في سلوكها عن الغاز المثالي عند 

الضغط  

- عند الضغط العالي بسبب أن زيادة الضغط يؤدي الى أجبار جسيمات الغاز على الاقتراب بعضها من بعض حتى يصبح من غير الممكن إهمال الحجم الذي تشغله الجسيمات وتتحول الغازات الحقيقية إلى سائل إذا تعرضت لضغط كاف

درجة الحرارة

- عند انخفاض درجة الحرارة تنخفض طاقة جسيماته  الحركية وهذا يعني أن قوی التجاذب تكون قوية بين جسيماته وهذا يؤثر في سلوك الغاز (تتحول الغازات الى سوائل عند انخفاض درجة الحرارة بقدر كاف ) 

قطبية الجسيمات

لا تسلك الغازات القطبية سلوك الغاز المثالي ( بسبب قوة التجاذب بين جسيماته تكون أكبر )

حجم الجسيمات 

كلما زاد حجم الغازات الغير قطبية تبتعد عن سلوك المثالي للغاز