حل درس قسمة الأعداد الصحيحة على كسور رياضيات سادس
التركيز تضييق النطاق
الهدف قسمة الأعداد الكلية على الكسور
الترابط المنطقي الربط داخل الصفوف وبينها
السابق
استخدم الطلاب النماذج لقسمة الاعداد الكلية على الكسور
الحالي
يعمل الطلاب على قسمه الأعداد الكلية على الكسور
التالي
سيعمل الطلاب على قسمة الكسور والأعداد الكلية
الدقة اتباع المفاهيم والتمرس والتطبيق
انظر المخططات البيانية لمستويات الصعوبة في الصفحة 309
المشاركة الاستكشاف الشرح التوضيح التقييم
1 بدء الدرس
أفكار يمكن استخدامها
قد تود أن تبدأ الدرس باستخدام مجموعة كاملة أو مجموعة صغيرة أو نشاط "فكر - اعمل في ثنائيات - شارك أو نشاط ذاتي.
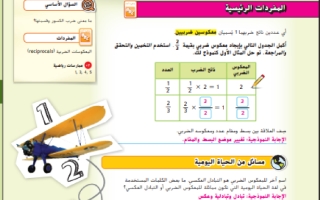
LA مناقشات ثنائية اطلب من الطلاب العمل في مجموعات ثنائية لإكمال المفردات الرئيسية، ذكرهم بأن المرادف هو بمثابة مصطلح له نفس المعنى المراد من مصطلح آخر. إذا المقلوبات والمعكوس الضريبي مترادفان. 7 ,6 ,1
الإستراتيجيات البديلة
أما إذا وجد الطلاب صعوبة، فوضح لهم أنهم يختارون الأعداد لإيجاد کسر يمثل 1، على سبيل المثال، يساوي الناتج 1
BL اطلب من الطلاب إكمال مسائل من الحياة اليومية ومناقشة متى يستخدمون المقلوبات خارج الفصل المدرسي أو غيرها من الوسائل التي يمكن أن تمثل بشكل مرئي مقلوبا ضربيا
2 تدريس المفهوم
اطرح أسئلة الدعائم التعليمية لكل مثال للتميز بين خيارات التعليم
أمثلة
1 - 3 . أوجد المقلوب.
AL . ماذا يقصد بالمقلوب عددان ناتج ضربهما يساوي 1
- ماذا يحدث للبسط والمقام عند كتابة المقلوب لكسر ما ؟ يتغير موقع البسط والمقام.
في المثال 1، ما العدد الذي عند ضربه في يساوي 1
في المثال 1. ما الناتج. المعبر عنه في صورة كسر، من ضرب و . في المثال 2، ما العدد الذي عند ضربه يساوي 821
في المثال 3. ما العدد الذي عند ضربه في 5 يساوي 1 ؟ 1 .
إذا تم التعبير عن كسر ما باستخدام الرمزين فما هو المطلوب لهما، معبرا عنه باستخدام الرموز و ما وجه الاختلاف بين المثال 3 والمثالين 1 و2 ؟
هل يتمثل هذا التغيير في كيفية إيجاد المطلوب ؟ العدد الموجود في المثال 3 هو عدد کلي. لا : العملية المطلوبة لإيجاد المقلوب هي نفسها بعدما تعبر عن العدد الكلي في صورة كسر.
هل تحتاج مثال آخر ؟ أوجد المقلوب لكل عدد
أمثلة
4. قسمة عدد کلي على كسر.
ماذا يمثل العمود بأكمله في النموذج العدد الكلي 2
كيف ينبغي أن تقسم كل عدد کلي ؟ إلى أثلاث
- كم عدد مجموعات الموجودة في 2 ؟ 0.
ما المقلوب
کیف يمکن إعادة كتابة في صورة تعبیر ضربي . أي طريقة تفضلها ؟ اشرح. راقب تفضيلات الطلاب.
لماذا يكون ناتج القسمة أكبر من العامل الأول ؟ نقوم بالقسمة على الكسر الذي يكون أصغر من 1، والذي هو نفسه عند ضرب الكسر في 3، والذي يكون أكبر من 1.
هل تحتاج لمثال آخر ؟ أوجد ناتج اكتب في أبسط صورة. 10
5. قسمة عدد کلي على كسر.
لماذا تكتب العدد 7 في صورة و يمكن التعبير عن عدد كلي في صورة كسر مقامه يساوي 1
ما مرادف المقلوب ؟ المعكوس الضريبي
ما المقلوب
كيف يمكن إعادة كتابة 7 في صورة تعبير ضريبي
لماذا ناتج القسمة أكبر من العامل الأول ؟ نقوم بالقسمة على الكسر ، الذي يكون أصغر من 1، والذي هو نفسه عند ضرب الكسر في 3، ، والذي يكون أكبر من 1.
هل تحتاج لمثال آخر ؟ أوجد ناتج : اكتب في أبسط صورة. 1
التركيز تضيق النطاق
الهدف استخدام النماذج لقسمة الكسور
الترابط المنطقي الربط داخل الصفوف وبينها
الحالي
يستخدم الطلاب النماذج لقسمة الكسور على الكسور
التالي
سيقوم الطلاب بقسمة الكسور على الكسور
الدقة اتباع المفاهيم والتمرس والتطبيقات
انظر المخططات البيانية لمستويات الصعوبة في صفحة 315
المشاركة الاستكشاف الشرح التوضيح التقييم
1 بدء النشاط العملي
من المقرر استخدام الأنشطة 1، 2 ،3 على أنها أنشطة جماعية. ثم تصميم النشاط لتقديم مزيد من الإرشادات الطلاب أكثر من النشاط 2
نشاط عملي 1
فكر - اعمل في ثنائيات - شارك اطلب من الطلاب العمل في مجموعات ثنائية لإكمال الخطوات من 1 الى 3 قد يستخدم الطلاب شرط الكسور أو الوسائل اليدوية الأخرى للحصول على فهم إضافي للمفهوم. اطلب من الطلاب الاستماع إلى الأسئلة التالية والإجابة عليها 1، 7 5
اطرح الأسئلة التالية :
لماذا تقسم الرسم البياني الأعمدة إلى 9 قطاعات
لماذا نظلل المقام
كم عدد تجمعات المقسوم عليها الموجودة في في المقسوم ؟ أربعة
نشاط عملي 2
فكر - اعمل في ثنائيات - شارك اطلب من الطلاب الانتظام في مجموعات ثنائية لإكمال الخطوات من 1 إلى 3 أمنح كل مجموعة ثنائية دقيقة واحدة للتفكير في كيفية الإجابة على كل خطوة. بعد ذلك اطلب منهم إكمال كل خطوة بمساعدة زملائهم. مع مناقشة كل خطوة بصوت مرتفع. اطلب من المجموعات الثنائية مشاركة أفكارهم واجاباتهم ونواتجهم شفهيا مع باقي الفصل : 1، 4
نشاط عملي 3
فكر - اعمل في ثنائيات - اكتب اطلب من الطلاب الانتظام في مجموعات ثنائية لاكمال الخطوات من 1 إلى 3 أطلب من الطلاب التعاون فيما بينهم وعقد المناقشات قبل كتابة إجابات الأسئلة الواردة أدناه بمفردهم. 4 ,1، 3
اطرح الأسئلة التالية :
اشرح قسمة بأسلوبك الخاص. الإجابة النموذجية : اقسم إلى جزئين متساويين. توجد مجموعتان إذا سيساوي ناتج القسمة .
اشرح بأسلوب لفظي ماذا يحدث عند قسمة كسر علی کسر. الإجابة النموذجية : إذا قمت بقسمة كسر أصغر من واحد، فإن ناتج القسمة سيكون أكبر من المقسوم. إذا قمت بقسمة كسر أكبر من واحد، فإن ناتج القسمة سيكون أصغر من المقسوم.
اللعب في مجموعات ثنائية اطلب من الطلاب العمل في مجموعات ثنائية لتصميم بطاقات الخط والمطابقة باستخدام البطاقات لأداء لعبة التذكر. امنح كل مجموعة ثنائية من الطلاب 10 بطاقات دليلية في 5 من البطاقات الدليلية، أطلب منهم كتابة تعبير القسمة الذي يتضمن الكسور. في البطاقات الخمس الأخرى، أطلب منهم رسم النموذج الذي يمثل التعبير. وجه كل البطاقات لأسفل. يرسم أحد الزملاء بطاقتين. إذا كان لديهم مطابقة، ليحتفظون بمجموعة البطاقات الثنائية. إذا لم يكن لديهم مطابقة، فسيوجهون البطاقات الأسفل مجددا ويرسم الزميل الثاني بطاقتين كرر العملية حتى يتم رسم جميع البطاقات. يفوز الطالب صاحب العدد الأكبر من المتطابقات 7
التحليل والتفكير
الرؤوس المرقمة معا اقسم الطلاب في مجموعات مكونة من 3 إلى 4 رقم کل طالب في الصورة 1 أو 2 أو 3 أو 4 ينبغي على كل مجموعة مصممة إكمال التمارين لضمان استيعاب كل فرد في المجموعة ينبغي على الطلاب طلب المساعدة والدعم من بعضهم البح عند الحاجة استدع طالبا مرقما لشرح نتائج مجموعات للفصل 1، 3
الابتكار
العصف الذهني في الوحدة بالكامل استخلص أفكارا من العصف الذهني في الوحدة بالكامل لإكمال التمرينين 14 ,17