حل درس ضرب أحاديات الحد وقسمتها رياضيات صف ثامن
التركيز تضييق النطاق
الهدف تبسيط تعابير الأعداد الحقيقية عن طريق ضرب أحاديات الحد وقسمتها.
الترابط المنطقي الريط داخل الصفوف وبينها
السابق
أوجد الطلاب قيمة التعابير التي تتضمن الأسس
الحالي
يستخدم الطلاب قوانین الأسس لضرب وقسمة أحاديات الحد.
التالي
يستخدم الطلاب قوانین الأسس لإيجاد قوة أسية لقوة اسية
الدقة اتباع المفاهيم والتمرس والتطبيق
انظر الرسم البياني لمستويات الصعوبة في صفحة 27
المشاركة الاستكشاف الشرح التوضيح التقييم
1 بدء الدرس
أفكار يمكن استخدامها
قد نود أن نبدأ الدرس باستخدام مجموعة كاملة أو مجموعة صغيرة أو نشاط "فكر - اعمل في ثنائبات - شارك" أو نشاط ذاتي.
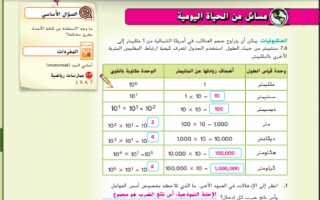
حلقات النقاش الجماعي اطلب من الطلاب العمل في فرق تتكون من ثلاثة طلاب لتوسيع النمط المعروض في الجدول. على سبيل المثال، يكمل الطالب الأول الإدخال الخاص بالسنتيمتر، ثم يمرره للطالب التالي لإكمال الإدخال الخاص بالديسيمتر، وهكذا إلى أن يكتمل الجدول، ثم يتناقش الطلاب بشأن الإجابات بالنسبة للتمرينين 1 و2 و 8 ,7 ,1
الإستراتيجية البديلة
اطلب من الطلاب البحث عن بادئات وحدات القياس وملاحظة أيها له جذور بونانية وأيها له جذور لاتينية. ثم اطلب من الطلاب تجميع قائمة من كلمات أخرى باللغة الإنجليزية تستخدم تلك الجذور . من 6 ,1
2 تلقين المفهوم
اطرح أسئلة الدعائم التعليمية لكل مثال للتمييز بين خيارات التعليم
أمثلة
1 - 2. أوجد ناتج القوى الأسية
في المثال 1، ما أس العامل الأول ؟ والعامل الثاني ؟
هل الأساسات متشابهة ؟ نعم
في المثال 2. هل الأساسات متشابهة ؟ نعم
في المثال 2. کیف ستبحث عن الأس في الإجابة ؟ أضف الأسس لكل عامل سويا 1 .
عند ضرب لماذا لا يكون معامل ناتج الضرب 2؟ عند الضرب، أنت لا تجمع المعاملات، بل تضربها. معاملات
هل تريد مثالا آخر ؟
حول كل تعبير إلى أبسط صورة باستخدام قوانين الأسس
أوجد ناتج القوى الأسية.
ما معاملات كل عامل ؟
ما أس العامل الأول والعامل الثاني عند إيجاد ناتج ضرب الحدین، ماذا تفعل بالمعاملات ؟ اضربها
عند إيجاد ناتج ضرب الحدین، ماذا تفعل الأسس إذا كانت الأساسات متشابهة ؟ اجمعها
ما الخصائص التي تسمح لك بإعادة تقسيم العوامل إلى مجموعات بحيث تكون المتغيرات سويا ؟ خاصية التجميع و التبديل في الضرب
حول لأبسط صورة
هل تريد مثالا أخر ؟
حول لأبسط صورة باستخدام قوانين الأسس
أمثلة
4 - 5 . أوجد ناتج قسمة القوى الأسية.
في المثال 4، ما أس البسط؟ 8
في المثال 4. ما أس المقام ؟ 2
هل الأساسات متشابهة ؟ نعم
ماذا تفعل لإيجاد أس ناتج القسمة ؟ اطرح 2 من 8
في المثال 5. هل الأساسات متشابهة ؟ نعم
في المثال 5. کیف سنجد الأس في الإجابة ؟ اطرح 4 من 9
عند قسمة القوى الأسية التي لها نفس الأساس، ماذا تفعل بالأسس والأساس ؟
اطرح الأسس، واحتفظ بالأساس كما هو
هل تريد مثالا آخر ؟
حول كل تعبير لأبسط صورة باستخدام قوانين الأسس
6. أوجد ناتج قسمة القوى الأسية.
ما الحدود التي لها نفس الأساس؟ 25 و25، 35 و 34، 5 و 5
أعد كتابة المسألة بحيث يتم تجميع الحدود حسب الأساسات المشتركة
كيف يمكن إعادة كتابة التعبير في صورة ضرب 3 کسور
كيف يكون كل عامل في أبسط صورة ؟ 5 ;3 حول لأبسط صورة
هل تريد مثالا آخر ؟ حول لأبسط صورة
مثال
7. أوجد ناتج قسمة القوى الأسية
ما الذي يتعين عليك إيجاده عدد المرات التي يزيد فيها طول ساحل هاواي عن ساحل نيوهاما - فهل ستحتاج إلى الجمع أم الطرح أم الضرب أم القسمة ؟ القسمة
ما مسألة القسمة التي تحتاج إلى حلها؟
ما العملية التي ستحتاج لاستخدامها لحل المسألة ؟
ما التعبير الذي يمثل هذه الحالة ؟
يزيد طول نهر المسيسيبي قليلا عن3 ، ميلا نهر بينما يبلغ طول نهر کانساس نحو و میلات تقريبا. وضح طريقة حل هذه المسألة دون تقييم الأعداد و القسمة راجع عمل الطلاب
هل تريد مثالا آخر ؟
يساوي الستيمتر الواحد 1 ملليمترات، بينما يساوي الكيلومتر 10 ملليمترات. فكم عدد السنتيمترات في الكيلومتر الواحد ؟ cm 10
تمرين موجه
التقويم التكويني استخدم هذه التمارين لتقويم استيعاب الطلاب للمفاهيم الواردة في هذا الدرس.
إذا كان بعض من طلابك غير مستعدين لإنجاز الواجبات فاستخدم الأنشطة المتمايزة الواردة أدناه.
مراجعة ثنائية اطلب من الطلاب العمل في مجموعات ثنائية الحل التمارين 13. يحل زميل المسألة أثناء قيام الأخر بالتوجيه، يمكن أن يختار المدرب تقديم المساعدة بأن يطلب من زميله تدوين التعابير أي ثم ينفذ العملية الملائمة. يتبادل الطلاب الأدوار في حل كل مسألة. بعد كل مسألتين، تتحقق المجموعات الثنائية من إجاباتها مع المجموعات الثنائية الأخرى ويناقشون أي اختلافات. 8، 0 ,7 ,6 ,13 0
مناقشات ثنائية اطلب من الطلاب العمل في أزواج لإكمال ورقة العمل الإثرائية "قسمة القوى الأسية ذات الأساسات المختلفة". ثم اطلب منهم مبادلة الحلول مع مجموعة ثانية أخرى من الطلاب و مناقشة أي اختلافات بينهما. 7
3 الممارسة والتطبيق
تمارين ذاتية وتمارين إضافية
تم إعداد صفحات التمارين الثانية بهدف استخدامها كواجب منزلي. يمكن استخدام صفحة التمرين الإضافي للتقوية الإضافية أو كواجب لليوم الثاني
مستويات الصعوبة
مستويات تقدم التمارين من 1 إلى 3 حيث يشير المستوى 1 إلى أقل مستوی من الصعوبة.
المستوى 3 المستوى 2 المستوى ا
الواجبات المقترحة
يمكنك استخدام الجدول أدناه الذي يحتوي على تمارين لكل مستويات الصعوبة لتحديد التمارين الملائمة لاحتياجات طلابك
خيارات الواجب المنزلي المتمایزة
قريب من المستوى 3. 11 فردي 35 34 ,2 ,2 ,21 ,20
ضمن المستوى 111 فردي. 35 ,24، 23، 2-1
أعلى من المستوى 3 ,2 ,3
خطأ شائع عند ضرب أحاديات الحد وقسمتها، يمكن أن يحاول الطلاب جمع أو طرح أسس القوى الأسية ذات الأساسات غير المتشابهة. ذكر الطلاب أن جمع الأسس و طرحها لا يحقق نتائج إلا إذا كانت الأساسات متماثلة.
ممارسات رياضية
التركيز على / ( التمرين التمارين )
ا فهم طبيعة المسائل والمثابرة في حلها 14, 22، 23، 19،16
3 بناء فرضیات عملية والتعليق على طريقة استنتاج الآخرين 21، 23
7 محاولة إيجاد البنية واستخدامها 20
تعد الممارسات الرياضية 1 و 3 و 4 جوانب من التفكير الرياضي الذي تم التركيز عليه في كل درس. امنح الطلاب الفرص لبذل الجهد الكافي لحل مسائلهم و التعبير عن استنتاجاتهم و تطبيق الرياضيات في مواقف من الحياة اليومية.
التقويم التكويني
استخدم هذا النشاط كتقويم تكويني نهائي قبل انصراف الطلاب من فصلك
بطاقة التحقق من استيعاب الطلاب
اطلب من الطلاب شرح طريقة تقييم الأساس عند ضرب الأعداد ذات الأساسات المتماثلة و قسمتها بصيغة أسية راجع عمل الطلاب