مذكرة وحدة الحركة الدورانية الفيزياء الصف الحادي عشر متقدم
اسم الطالب : ................................... المادة : الفيزياء
الصف و الشعبة : الحادي عشر المتقدم ( ........ ) عنوان الدرس : الوحدة ( 10 ) الحركة الدورانية
اليوم و التاريخ : العام الدراسي 2021 - 2022 الفصل الدراسي : الثالث
مدرسة الراشد الصالح الخاصة – دبي
( 1.10 ) الطاقة الحركية للدوران المحوري – صفحة ( 285 )
الحركة الدورانية: - هي حركة إلتفاف الجسم حول محور يمر بالجسم ، انظر الاشكال المجاورة .
ملاحظة ( في الشكل المجاور نلاحظ ما يلي : -
* الحركة الدائرية هي حركة ( الكرة الحديدية ) على محيط دائرة ، بينما الحركة الدورانية هي حركة ( الرجل ) حول محور يمر به ( حول نفسه ).
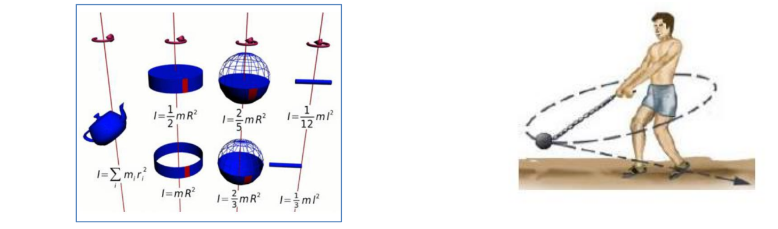
**حساب الطاقة الحركية للدوران المحوري لحركة جسيم نقطي على محيط دائرة نصف قطرها ( r ) حول محور ثابت ، كما في الشكل المجاور .
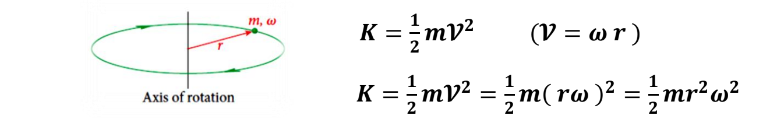
_ قانون حساب الطاقة الحركية للدوران المحوري لحركة جسيم نقطي على محيط دائرة نصف قطرها ( r ) حول محور ثابت : -

الحركة الدائرية لعدة جسيمات نقطية – صفحة ( 286 )
* تُحدد الطاقة الحركية للدوران المحوري لجسيم نقطي واحد يتحرك حركة دائرية حول ثابت بالعالقة : -
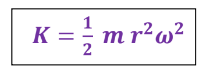
** إذا كان لدينا عدة جسيمات نقطية تتحرك حركة دائرية حول محور دوران ثابت ،حيث أنها تحتفظ بمسافات ثابتة
فيما بينها و كذلك مسافات ثابتة بينها و بين محور الدوران المشترك لها .كما في الشكل المجاور.
لذلك يكون لجميع جسيمات النظام السرعة الزاويّة نفسها ( ω.)
في هذه الحالة تكون الطاقة الحركية الكلية للنظام تساوي مجموع الطاقات الحركية الفردية لجسيمات النظام ، أي أن : -
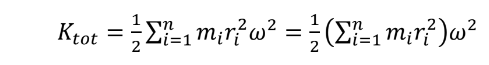
ولكن تسمى :
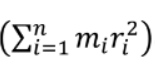
عزم القصور الذاتي و كذلك تسمى القصور الدوراني و رمزها ( I ) و تعتمد هذه الكمية فقط على كتل
الجسيمات الفردية ( mi ) و المسافات التي تفصلها عن محور الدوران ( ri للتربيع )
** لذلك يمكن حساب عزم القصور الذاتي لنظام يتكّون من مجموعة جسيمات نقطية تدور حول محور ثابت
باستخدام القانون التالي : -
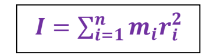
( I ) عزم القصور الذاتي للنظام ، و يُقاس بوحدة ( Kg . m2 )
( mi ) كتلة كل جسيم من مكونات النظام ، و يُقاس بوحدة ( Kg. )
( ri للتربيع ) مربع المسافة بين الكتلة و محور الدوران .
*** فيكون قانون حساب الطاقة الحركية للدوران المحوري لنظام يتكون من مجموعة من الجسيمات النقطية
تتحرك حركة دائرية حول محور دوران مشترك كما يلي : -
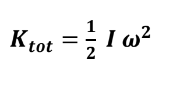
مراجعة المفاهيم ( 1.10 ) _ صفحة ( 286 ) ] فكر في كتلتين متساويتين ( m ) متصلتين بساق رفيع عديم الكتلة ، كما في الاشكال المجاورة ، تدور الكتلتان في مستوى أفقي حول محور رأسي يمثل بخط متقطع ، ما النظام
الذي يحظى بأعلى عزم قصور ذاتي ؟

الحل - قانون عزم القصور الذاتي أو القصور الدوراني لنظام يتكون من مجموعة جسيمات نقطية هو
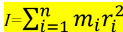
بما ان النظام يتكون من كتلتين, لذلك يمكن كتابة القانون بالشكل التالي : -
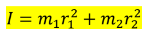
نفرض المسافة بين الكتلتين ( d ) .
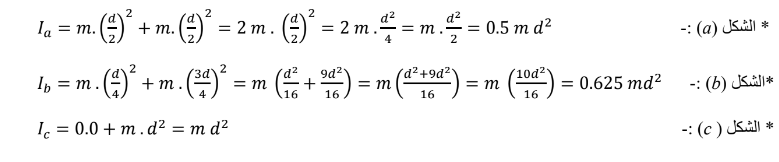
سؤال ( 39.10 ) صفحة ( 318 ) حدد عزم القصور الذاتي لثلاثة مراهقين كتلة كل منهم
( m1 = 60 kg m2 = 45 kg m3 = 80 kg ) يجلسون في نقاط مختلفة على حافة منصة دوارة نصف
قطرها ( 12.0 m ) كما في الشكل المجاور ؟
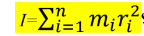
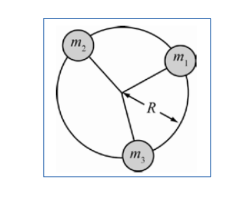
الحل :
سؤال (1 ) أربعة أجسام كروية جوفاء كتلة كل منها ( 1Kg ) ونصف قطرها ( cm 10 = R ) متصلة بقضبان عديمة
الكتلة لتُش كل مربعًا بأضالع طولها ( cm 50=L .) إذا كانت الكتل تدور حول محور يُنصف ضلعين من أضلاع المربع ، كما في الشكل المجاور. احسب عزم القصور الذاتي للنظام ؟
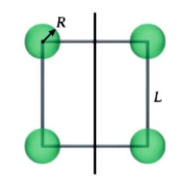
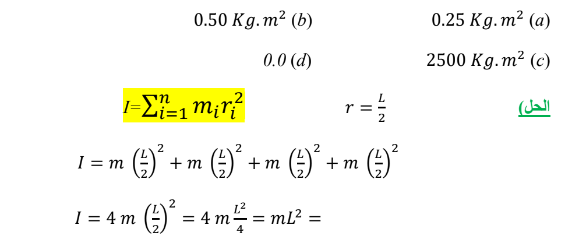
سؤال ( 2 ) أربعة أجسام كروية جوفاء كتلة كل منها ( 1Kg ) و نصف قطرها ( cm 10=R ) متصلة بقضبان عديمة
الكتلة لتُشكل مربعًا بأضلاع طولها ( cm 50=L .) إذا كانت الكتل تدور حول محور يمر عبر الخط القطري للمربع ،كما
في الشكل المجاور. احسب عزم القصور الذاتي للنظام ؟
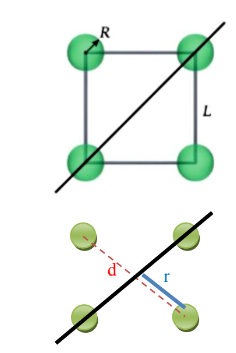

سؤال ( 4.10 ) صفحة ( 316 ) أربعة أجسام كروية جوفاء كتلة كل منها ( 1Kg ) و نصف قطرها ( cm 10=R )
متصلة بقضبان عديمة الكتلة لتُش ّكل مربعًا بأضلاع طولها ( cm 50=L .) في الحالة الاولى تدور الكتل حول محور
يُنصف ضلعين من أضلاع المربع ، و في الحالة الثانية تدور الكتل حول محور يمر عبر الخط القطري للمربع . كما هو
موضح في الشكل ، احسب نسبة عزم القصور الذاتي في الحالتين ؟
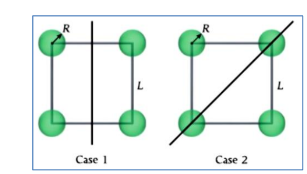
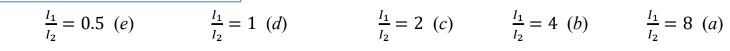
سؤال ( 5.10 ) صفحة ( 316 ) إذا استبدلنا بالاجسام الكروية الجوفاء في السؤال ( 4.10 ) أجساما كروية صلبة لها
الكتلة و نصف القطر أنفسهما ، فإن نسبة عزم القصور الذاتي في الحالتين سوف ؟
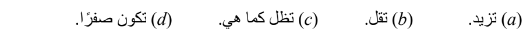
( 2.10 ) حساب عزم القصور الذاتي – صفحة ( 286 )
دوران جسم صلب حول محور ثابت يمر عبر مركز الكتلة
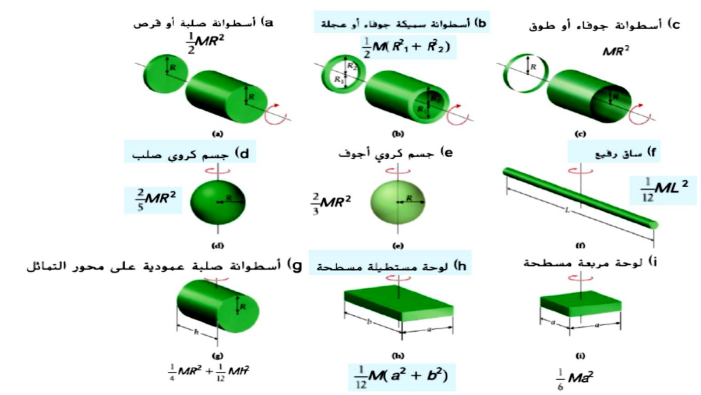
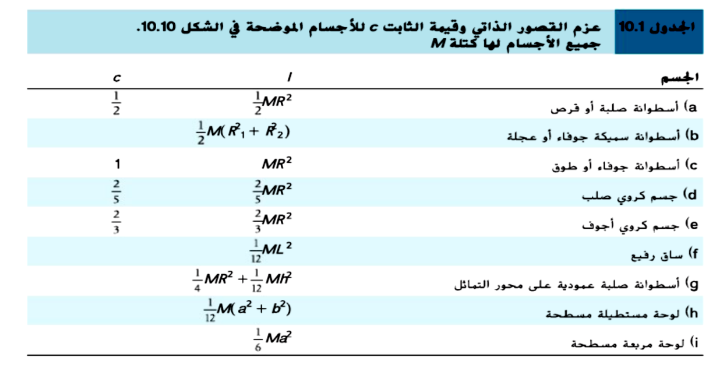
* عزم القصور الذاتي لجسم صلب يدور حول محور يمر عبر مركز كتلته تختلف قيمته وفقا للشكل الهندسي
للجسم ، حيث : -
****** عزم القصور الذاتي لجميع الاجسام المستديرة هو : -
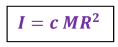
( c ) ثابت قيمته تختلف وفقا للشكل الهندسي للجسم الصلب ، حيث
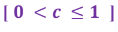
و تُعطى قيمته و لا تُحفَظ .
ملاحظة ( اشتقاق القوانين غير مطلوب ، و كذلك القوانين تُعطى و لا تُحفَظ
** حساب الطاقة الحركية للدوران المحوري لجسم صلب
ملاحظة مهمة ) يمكن اعتبار الجسم الصلب نظام يتكّون من مجموعة جسيمات نقطية ، لذلك يمكن استخدام
القانون التالي لحساب الطاقة الحركية للدوران المحوري لاي جسم صلب ، حيث : -
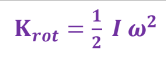
( Krot ) الطاقة الحركية للدوران المحوري لجسم صلب يدور حول محور ثابت يمر في مركز الكتلة.
( I ) عزم القصور الذاتي للجسم الصلب ( لكل جسم صلب قانون خاص به حسب شكله الهندسي ، و القانون
يُعطى و لا يُحفَظ )
( w مربع ) مربع السرعة الزاوية للجسم الصلب

سؤال ( 3.10 ) صفحة ( 316 ) حدافة مولد ، و هي أسطوانة صلبة متجانسة نصف قطرها (R) و كتلتها ( M ) و عزم القصور الذاتي لها
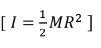
تدور حول محورها الطولي ، و السرعة الخطية لنقطة ما على الحدافة هي ( θ ) ، ما مقدار الطاقة الحركية للحدافة ؟
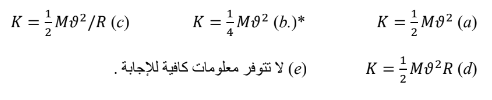
سؤال ( 7.10 ) صفحة ( 316 ) توجد اسطوانة صلبة و أخرى جوفاء تدوران حول محور يمر عبر مركز الكتلة بهما ، إذا
كان الجسمان متماثلين من حيث الكتلة و نصف القطر ، فما الجسم الذي سيحظى بأكبر عزم قصور ذاتي ؟
(ملاحظة : - انظر الجدول 1.10.)
أ - سيكون عزم القصور الذاتي متماثلا في الجسمين.
ب - ستحظى الأسطوانة الصلبة بأكبر عزم قصور ذاتي لأن كتلتها موزعة بانتظام .
ج - ستحظى الأسطوانة الجوفاء بأكبر عزم قصور ذاتي لأن كتلتها تقع بعيدا عن محور الدوران..
د - لا يمكن التنبؤ بذلك لعدم وجود معلوات كافية
سؤال ( 18.10 ) صفحة ( 317 ) ما العبارة الصحيحة حول عزم القصور الذاتي لجسم صلب غير نقطي مما يلي ؟
أ - عزم القصور الذاتي مستقل عن محور الدوران
ب - عزم القصور الذاتي يعتمد على محور الدوران
ج - عزم القصور الذاتي يعتمد على كتلة الجسم فقط.
د - عزم القصور الذاتي يعتمد فقط على أكبر بعد عمودي للجسم
سؤال ( 10.10 ) صفحة ( 316 ) تتدحرج أسطوانة لأسفل دون انزلاق على مستوى يميل بزاوية ( θ ) بالنسبة إلى
المستوى الأفقي ، ما مقدار الشغل المبذول من قوة الاحتكاك أثناء انتقال الأسطوانة مسافة ( S ) على امتداد
المستوى. ( �� هو معامل الاحتكاك السكوني بين المستوى و الأسطوانة )
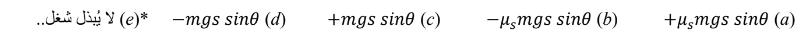
سؤال ( 14.10 ) صفحة ( 316 ) تدور متزلجة جليدية باسطة ذراعيها ثم تضمهما مما يجعلها تدور بشكل أسرع ، ما
العبارة الصحيحة مما يلي ؟
أ - لا تتغير الطاقة الحركية للدوران لديها ألن الجزء الذي تزيده سرعتها الزاوية مماثل للجزء الذي يقلله قصورها
الذاتي .
ب - تزداد الطاقة الحركية للدوران لديها بسبب الشغل الذي تبذله لضم ذراعيها..
ج - تقل الطاقة الحركية للدوران لديها بسبب انخفاض قصورها الذاتي ، إذ تفقد الطاقة لانها تُجهد بصورة
تدريجية .
سؤال ( 17.10 ) صفحة ( 317 ) تسير دراجة بسرعة ( s/m 4.02 )فإذا كان نصف قطر العجلة الامامية ( m 0.450 )
فما المدة التي تستغرقها هذه العجلة للقيام بدورة كاملة ؟
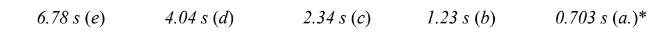
( 3.10 ) التدحرج دون انزلاق – صفحة ( 293 )
حركة التدحرج : - هي حالة خاصة للحركة الدورانية تقوم بها أجسام مستديرة نصف قطرها ( R ) و تتحرك عبر
سطح من دون انزلاق .
*يمكن وصف حركة التدحرج بأنها مزيج من الحركة الدورانية للجسم بالاضافة إلى الحركة الانتقالية لمركز كتلته .
* الطاقة الحركية الكلية ( K ) لجسم في حركة التدحرج هي مجموع طاقته الحركية الانتقالية ( Krans ) الناتجة
عن الحركة الخطية لمركز كتلته و طاقته الحركية الدورانية ( Krot ) الناتجة عن دوران الجسم حول مركز كتلته أي
أن : -
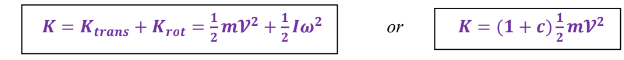
_ ملاحظات مهمة حول هذا القانون
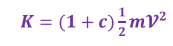
* مقدار الطاقة الحركية ( K ) لاي جسم مستدير ( كرة أو أسطوانة ) متدحرج يعتمد على : -
( 1 ) مربع السرعة الخطية لمركز كتلة الجسم
( 2 ) كتلة الجسم ( m.)
( 3 ) قيمة الثابت ( c ) الذي تختلف قيمته باختلاف التوزيع الهندسي للكتلة و كذلك باختلاف طبيعة الجسم
(صلب أو أجوف).
مراجعة المفاهيم ( 2.10 ) صفحة ( 294 ) جسم كروي صلب و أسطوانة صلبة و أسطوانة جوفاء متماثلة من حيث
الكتلة و نصف القطر و تتدحرج بالسرعة نفسها ، ما العبارة الصحيحة مما يلي :- ( ملاحظة: - انظر الجدول ( 10.1 )
أ - الجسم الكروي الصلب به أعلى طاقة حركية .
ب - الاسطوانة الصلبة بها أعلى طاقة حركية.
ج - الاسطوانة الجوفاء بها أعلى طاقة حركية.
د - جميع الاجسام الثالثة لها طاقة حركية مماثلة .
سؤال( 20.10 ) صفحة ( 317 ) تتدحرج أسطوانة صلبة و أسطوانة جوفاء و جسم كروي صلب و جسم كروي أجوف
دون انزلاق ، الاجسام الاربعة متماثلة من حيث الكتلة و نصف القطر و تنتقل بالسرعة الخطية نفسها ، ما العبارة
الصحيحة مما يلي ؟
أ - الاسطوانة الصلبة بها أعلى طاقة حركية .
ب - الاسطوانة الجوفاء بها أعلى طاقة حركية ..
ج - الجسم الكروي الصلب به أعلى طاقة حركية.
د - الجسم الكروي الاجوف به أعلى طاقة حركية.
و - الاجسام الاربعة لها الطاقة الحركية نفسها.
سؤال ( 10.38 ) صفحة ( 318 ) اسطوانة صلبة منتظمة كتلتها ( M = 5.00 Kg ) تتدحرج دون انزلاق على طول
سطح افقي , سرعة مركز كتلتها ( 30.0 m/s ) احسب طاقتها ؟ حيث
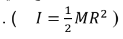
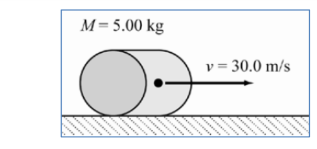
الحل : للاسطوانة حركتين هما :
_ حركة انتقالية : لمركز كتلتها, فيكون لها طاقة حركة انتقالية , حيث : -
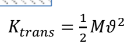
_ حركة دورانية : حول محور يمر عبر مركز كتلتها, فيكون لها طاقة حركية للدوران المحوري , حيث : -
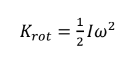
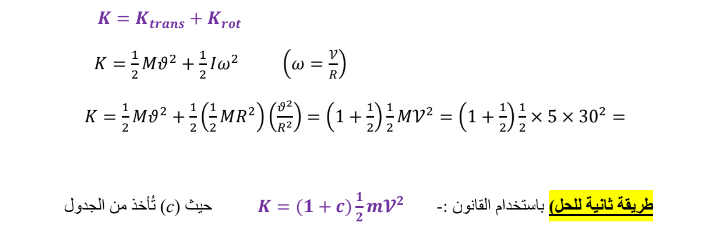
مسألة محلولة ( 10.1 ) صفحة ( 294 ) جسم كروي صلب كتلته ( Kg 5.15 ) و نصف قطره ( m 0.340 ) يبدأ الحركة
من السكون على ارتفاع ( m 2.10 ) فوق قاعدة مستوى مائل و يتدحرج لاسفل دون انزلاق تحت تأثير الجاذبية ،
ما السرعة الخطية لمركز كتلة الجسم الكروي عندما يغادر المستوى المائل و يتدحرج على سطح أفقي ؟
الحل ( بتطبيق قانون حفظ الطاقة الميكانيكية ، حيث : -
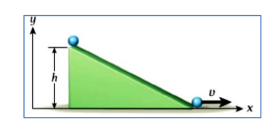

_ ملاحظات مهمة حول القانون :

( v ) مقدار السرعة الخطية لجسم مستدير ( كرة أو أسطوانة ) متدحرج عند أسفل سطح مائل .
( h ) ارتفاع السطح المائل.
(c ) قيمة الثابت ، تُأخذ من الجدول .
1 - مقدار السرعة الخطية ( v ) يعتمد على ارتفاع السطح المائل ( h. )
2 - مقدار السرعة الخطية ( v ) لا يعتمد على كتلة الجسم و إنما يعتمد على التوزيع الهندسي للكتلة الذي
يمثله الثابت ( c )حيث قيمته تختلف باختلاف طبيعة الجسم ( صلب أو أجوف ).
3 - كلما زادت قيمة الثابت ( c ) يقل مقدار السرعة الخطية ( v )
مثال ( 10.2 ) صفحة ( 295 ) جسم كروي صلب و أسطوانة صلبة و أسطوانة جوفاء ( أنبوب ) ، كلها بالكتلة
نفسها و لها نصف القطر الخارجي نفسه ( R ) تم تحريرها من وضع السكون في قمة السطح المائل و بدأت
في التدحرج دون انزلاق ، فما ترتيب وصولها إلى أسفل السطح المائل ؟ ( ارجع إلى الجدول ( 10.1 )لمعرفة قيمة
الثابت ) c ]

أ - الاجسام الثلاثة تصل في اللحظة نفسها .
ب - الجسم الكروي الصلب يصل أولا ، ثم الاسطوانة الصلبة ، و أخيرا الاسطوانة الجوفاء.
ج - الاسطوانة الصلبة تصل أولا ، ثم الجسم الكروي الصلب ، و أخيرا الاسطوانة الجوفاء.
د - الاسطوانة الجوفاء تصل اولا ، ثم الاسطوانة الصلبة ، و أخيرا الجسم الكروي الصلب.
سؤال ( 10.1 ) صفحة ( 316 ] ) يبدأ جسم مستدير من حالة السكون و يتدحرج دون انزلاق على مستوى مائل، عبر
مسافة رأسية تساوي ( 4.0 m ) و عند وصول الجسم إلى القاع فإن سرعته الانتقالية تكون ( s/m 7.0 ) ما الثابت
( C ) الذي يربط عزم القصور الذاتي بكتلة هذا الجسم و نصف قطره ؟
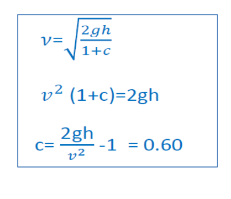
أ - 0.89
ب - 0.60
ج - 0.40
د - 0.20
سؤال ( 10.2 ) صفحة ( 316 ] ) كرتان من الفولاذ الصلب إحداهما صغيرة و الاخرى كبيرة، على مستوى مائل.قطر
الكرة الكبيرة أكبر مرتين من قطر الكرة الصغيرة ،و مع البدء من السكون تتدحرج الكرتان دون انزلاق على
المستوى المائل حتى حتى يكون مركزا كتلتيهما ( m 1 ) أسفل موضعي البدء ، ما سرعة الكرة الكبيرة ( v1 )
مقارنة بسرعة الكرة الصغيرة ( v2 ) بعد التدحرج لمسافة ( m 1 ) ؟

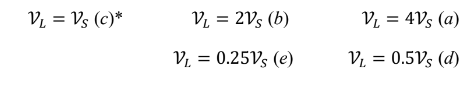
سؤال( 10.9 ) صفحة ( 316 ] ) جسم كروي صلب يتدحرج دون انزلاق على مستوى مائل ، و يبدأ من حالة السكون ،
في الوقت نفسه يبدأ صندوق من حالة السكون على الارتفاع نفسه و ينزلق على المستوى المائل نفسه ، مع
احتكاك ضئيل ، ما الجسم الذي سيصل إلى القاع اولا ؟
أ - سيصل الجسم الكروي الصلب اولا.
ب - سيصل الصندوق اولا..
ج - كلاهما سيصل في الوقت نفسه .
د - من المستحيل تحديد ذلك
توضيح الحل : سرعة الجسم الكروي عند اسفل السطح المائل تساوي : -

بينما سرعة الصندوق عند اسفل السطح المائل تساوي : -
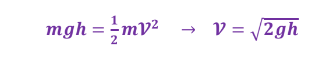
( 10.4 ) عزم الدوران صفحة ( 297 )
عزم الدوران ( τ ) : - هو مقدرة كل من القوة و ذراع العزم على إحداث دوران الجسم . و ينتج عن الضرب الاتجاهي
لمتجه القوة ( F ) و متجه ( ذراع العزم أو متجه الموقع ( r ) r × F = τ
ذراع العزم أو متجه الموقع ( r ) :- المسافة العمودية من محور الدوران ( نقطة الاصل ) إلى موقع تأثير القوة.
* يمكن حساب مقدار العزم باستخدام القانون التالي : -

وحدة قياس العزم ( m . N. )
ملاحظات حول القانون :
- نلاحظ من القانون أن مقدار العزم ( τ ) يتناسب طرديا مع كل من : -
* ذراع العزم أو ( r ) .
** مقدار القوة ( F )
*** Sin θ ( θ ) هي الزاوية المحصورة بين متجه القوة و متجه ( ذراع العزم أو متجه الموقع ) .
سؤال ( 1 ] ) الاشكال التالية توضح شخص يستخدم مفتاح لفك برغي ، ناقش الحالات الثلاث ؟ و في أي منها
يستطيع الشخص فك البرغي بسهولة ، مفسرا إجابتك ؟

الشكل( a ) : - عزم الدوران يساوي صفر ، لان متجه القوة يوازي متجه الموقع ( ذراع العزم ) أي أن ( 0.0 = θ ) و
( 0.0 = 0 sin ) فإن ( τ = 0.0 )
الشكل( b ) : - من الصعوبة فك البرغي ، لان ذراع العزم ( r ) قصير ( المسافة من محور الدوران (موقع الرغي )
إلى خط عمل القوة ( موقع اليد) قصيرة ) فيكون مقدار العزم قليل .
الشكل ( c ) : - يوضح الشكل الاستخدام الامثل للمفتاح حيث يَسهل فك البراغي لان ذراع العزم (r ) كبير، وكذلك
الزاوية بين متجه القوة و متجه ذراع العزم تقريبا قائمة ( 90 = θ ) و ( 1 = 90 sin ) فيكون عزم الدوران عند أقصى قيمة له
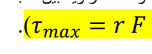
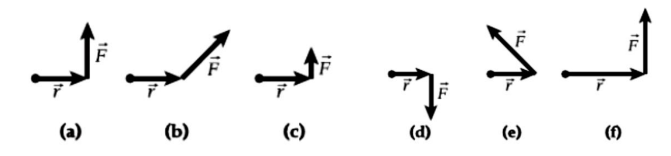
مراجعة المفاهيم ( 10.4 ) صفحة ( 298 ] ) أختر مزيجا من متجه الموقع ( r ) و متجه القوة ( F ) ينتج عزم الدوران
لاعلى مقدار حول النقطة التي تشير إليها النقطة السوداء ؟
ملاحظات : -
1 - عزم الدوران ( τ ) يُعَد متجه محوري ( المتجه المحوري هو متجه يُشير إلى محور الدوران ) .
2 - نحصل على اتجاه عزم الدوران باستخدام قاعدة اليد اليُمنى ، كما في الشكل المجاور، حيث يكون
الابهام باتجاه متجه الموقع ( r ) و تكون السبابة ( أو الاصابع الاربعة ) باتجاه متجه القوة ( F ) فتشير
الوسطى ( أو القلم ) إلى اتجاه عزم الدوران .
3 - متجه عزم الدوران ( τ ) يكون دائما عموديًا على كل من متجه الموقع ( r ) و متجه القوة ( F )
4 - الدوران حول أي محور ثابت قد يكون في اتجاه عقارب الساعة أو عكس اتجاه عقارب الساعة ، كما في
الشكل المجاور، فإن الدوران المتولد من اليد التي تسحب مفتاح الربط سيكون عكس اتجاه عقارب الساعة .
5 - محصلة الدوران ( τnet ) :- هي الفرق بين مجموع كل قيم العزم في اتجاه عقارب الساعة و مجموع كل
قيم العزم في عكس اتجاه عقارب الساعة . أي أن :-


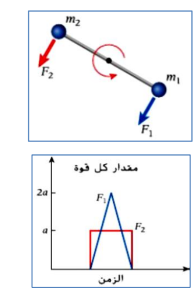
سؤال( 10.6 ) صفحة ( 316 ] ) جسم غير نقطي يتالف من كتلتين نقطيتين، ( m1 , m2 ) متصلتين عبر
ساق صلب عديم الكتلة طوله ( L )كما هو موضح في الشكل. يدور الجسم بسرعة زاويّة ثابتة حول محور
متعامد على الصفحة عبر نقطة منتصف الساق. و تُستخدم قوتان مماستان متفاوتتان في الزمن ( F1 , F2 )
في ( m1 , m2 ) على التوالي . و بعد استخدام القوتين ، ما الذي سيحدث للسرعة الزاويّة للجسم ؟
أ - سوف تزيد.
ب - سوف تقل.
ج - سوف تظل دون تغيير.
د - لا توجد معلومات كافية للتحديد.
سؤال( 10.47 ) صفحة ( 318) السؤال معدّل ) [ قرص كتلته ( 30.0 Kg ) و نصف قطره (40.0 cm ) مثبت في محور
أفقي عديم الاحتكاك ، و قد لف حبل عدة مرات حول القرص ثم ربط في قالب ( 70.0 Kg ) كما هو موضح في
الشكل، أوجد مقدار عزم الدوران المؤثر على القرص ؟

الحل : -
( 10.5 ) قانون نيوتن الثاني للدوران المحوري – صفحة ( 298 )
_ القانون الاول لنيوتن في الحركة الخطية : - إذا كانت محصلة القوى ( Fnet ) المؤثرة على جسم متحرك على خط مستقيم تساوي صفر فإن الجسم سوف يتحرك بسرعة خطية ( ) ثابتة .
a = 0.0 - - - - Fnet = 0.0
_ القانون الثاني لنيوتن في الحركة الخطية : - إذا أثرت على جسم محصلة قوى ( Fnet ) فإنه سوف يتحرك بعجلة ( α ) . Fnet = m a
_ _ القانون الاول لنيوتن في الحركة الدائرية : - إذا كانت محصلة عزم الدوران ( τnet ) المؤثرة على جسم يتحرك
في مسار دائري تساوي صفر، فإن الجسم سوف يتحرك بسرعة زاويّة ثابتة ، فتكون عجلته الزاويّة صفرا ، أي يكون
الجسم في حالة إتزان دوراني .
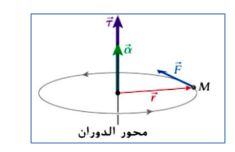
_ _ القانون الثاني لنيوتن في الحركة الدائرية : - في الشكل المجاور، جسيم نقطي كتلته ( M ) يتحرك في مسار
دائري نصف قطره ( r )بتأثير قوة ( F ) لذلك سوف يتأثر الجسيم بعزم دوران ( Sin θ τ = r F ) فيكون له عجلة
زاويّة ( α )
الصيغة الرياضية للقانون الثاني لنيوتن في الحركة الدائرية : -
τ = I α = r F sin θ
( τ ) عزم الدوران
( I ) عزم القصور الذاتي
( α ) العجلة الزاوية
( r ) نصف قطر المسار الدائري
( θ ) الزاوية بين القوة ( F ) و ( r )

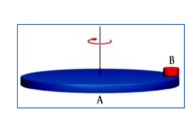
سؤال ( 10.51 ) صفحة ( 319 ] ) يدور جسم مكّون من جزأين على شكل قرص ( A , B ) كما هو موضح في الشكل،
حول محور عبر مركز القرص ( A ) إذا كان عزم الدوران المحوري الناتج عن الاحتكاك هو ( 0.200 N . m ) و عزم
القصور الذاتي للجسم ( 0.072 Kg . m ) فما المدة التي يستغرقها الجسم حتى يتوقف إذا كان يدور بسرعة زاويّة
إبتدائية تساوي ( ) ؟
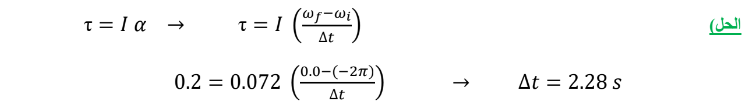

( 10.7 ) كمية الحركة الزاويّة – صفحة ( 306 )
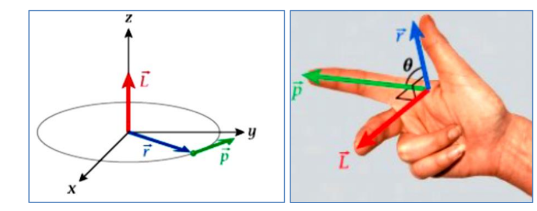
_ كمية الحركة الزاويّة للجسيم النقطي ( L ) :- هي الضرب الاتجاهي لمتجه الموقع ( r ) و متجه كمية الحركة ( p )
L = r × p
_ لذلك يمكن حساب مقدار كمية الحركة الزاويّة باستخدام القانون التالي : -
L = r p sin θ
(.θ ) الزاوية بين متجه الموقع ( r ) و متجه كمية الحركة ( p )
_ يمكن تحديد اتجاه كمية الحركة الزاويّة ( L ) باستخدام قاعدة اليد اليمنى ، حيث يكون الابهام باتجاه متجه
الموقع ( r ) و تكون السبابة ( او الاصابع الاربع ) باتجاه كمية الحركة ( p ) فتشير الوسطى ( او القلم ) الى
اتجاه كمية الحركة الزاوية ( L ) انظر الشكل المجاور
_ - معدل تغير كمية الحركة الزاويّة أو مشتقة الزمن لمتجه كمية الحركة الزاويّة تساوي عزم الدوران ، أي أن : -
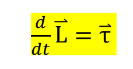
_ كمية الحركة الزاويّة للجسم الصلب ( L )
عندما يدور الجسم الصلب حول محور ثابت بسرعة زاوية ( ω ) فإن كمية الحركة الزاويّة ( L ) تتناسب ط
رديا مع السرعة الزاوية ، و يكون ثابت التناسب هو عزم القصور الذاتي للجسم الصلب ( I ) ، أي أن : -


حفظ كمية الحركة الزاويّة – صفحة ( 309 )
_ * بما أن معدل تغير كمية الحركة الزاويّة أو مشتقة الزمن لمتجه كمية الحركة الزاويّة تساوي عزم الدوران: -
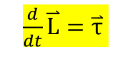

مثال ( 10.7 ) صفحة ( 310 ) موت نجم
في نهاية حياة نجم عملاق يبلغ خمسة اضعاف حجم الشمس, يكون لب النجم بالكامل تقريبا من فلز الحديد و بمجرد الوصول الى هذه المرحلة يصبح اللب غير مستقر و ينهار ( كما يوضح الشكل 10.31) خلال هملية تستغرق حوالي ثانية فقط و تكون بمثابة المرحلة الاولى لانفجار المستعر الاعظم من بين اكبر الاحداث التي تطلق الطاقة العظمى في الكون و يعتبر انفجار المستعر الاعظم مصدر اغلب العناصر الاثقل من الحديد و يطلق هذا الانفجار الحطام بما فيه العناصر الثقيلة في الفضاء الخارجي و قد يترك خلفه نجماً نيوترونياً يتكون من مواد نجمية مضغوطة الى كثافة اثقل بملايين المرات من اكبر الكثافات التي تم اكتشافها على الارض
المسأله : اذا كان اللب الحديدي يدور بمعدل ( 9.00 ) دورات في اليوم ، و إذا تناقص نصف قطره خلال الانهيار بمعامل ( 700 ) فكم تبلغ السرعة الزاويّة للب في نهاية الانهيار ؟ علما بأن عزم القصور الذاتي للب الحديدي يتناسب طرديًا مع مربع نصف قطره أثناء عملية الانهيار. و أن محصلة عزم الدوان الخارجي المؤثرة في اللب تساوي صفرا .
المعطيات :


10.12 لنفترض انك تبسط بكرة كابل كبيرة , إذا سحبت الكابل باستخدام شد ثابت فمائا سيحدث للعجلة الزاوية و السرعة الزاوية للبكرة. مع افتراض بقاء نصف القطر الذي تسحب منه الكابل ثابتاً و انعدام قوة الاحتكاك ؟
أ - يزداد كلاهما عند بسط البكرة
ب - يقل كلاهما عند بسط البكرة
ج - تزداد العجلة الزاوية بينما تقل السرعة الزاوية
د - تقل العجلة الزاوية بينما تقل السرعة الزاوية
و - يستحيل معرفة ذلك





