أوراق عمل مع الحل وحدة المجالات المغناطيسية للتيار فيزياء الصف الثاني عشر متقدم
أوراق عمل مع الحل وحدة المجالات المغناطيسية للتيار
قانون بيو سافار
مقدمة :
العالم ( هانز أورستد) لاحظ أنه عند مرور تيار كهربائي في موصل فإنه يتولد عنه مجالاً مغناطيسياً وقد وجد أن شكل المجال يختلف باختلاف شكل الموصل ( استطاع تحويل الطاقة الكهربائية إلى مغناطيسية )
إبرة البوصلة : دائماً يشير قطبها الشمالي إلى اتجاه خطوط المجال المغناطيسي كما أن اتجاه انحراف الإبرة يتوقف على عاملين هما
1- اتجاه مرور التيار في الموصل
2- وضع السلك بالنسبة للأبرة
عندما ينعكس اتجاه التيار المار في الموصل ينعكس اتجاه المجال المغناطيسي
عندما ينعكس اتجاه التيار ينعكس اتجاه المجال المغناطيسي
المجالات المغناطيسية الناتجة عن مرور التيار
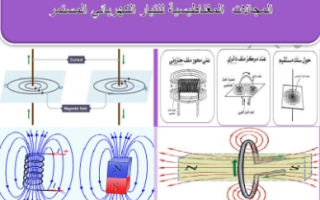
أولاً : المجال المغناطيسي الناشئ عن مرور تيار في سلك مستقيم
وصف المجال : دوائر منتظمة متحدة المركز مركزها هو السلك المار به التيار كما ان مستواه يكون عمودياً على التيار
تحديد اتجاه المجال :
قاعدة اليد اليمنى الثالثة أو قبضة اليد اليمنى
حيث يشير اصبع الأبهام لاتجاه التيار i بينما يشير انحناء باقي الأصابع لاتجاه خطوط المجال حول السلك
المماس عند أي نقطة يحدد اتجاه المجال المغناطيسي عند تلك النقطة
كذلك يمكن تحديد اتجاه المجال المغناطيسية عند أي نقطة باستخدام القاعدة الأولى لليد اليمنى
حيث يشير أصبع الأبهام إلى اتجاه عنصر التيار التفاضلي وأصبع السبابة تشير إلى اتجاه الموقع r وإصبع الوسطى يشير إلى اتجاه المجال المغناطيسي التفاضلي dB
في حال مرور التيار في سلكين متوازيين
التيار في اتجاه واحد
تنشأ قوة تجاذب بين السلكين ونستدل على ذلك بتطبيق قاعدة قبضة اليد اليمنى على كل سلك على حدة نجد أن B1 ,B2 بين السلكين في اتجاهين متضادين فتنشأ قوة تجاذب بينهما
التيار في اتجاهين متضادين
تنشأ قوة تنافر بين السلكين ونستدل على ذلك بتطبيق قاعدة قبضة اليد اليمنى على كل سلك على حدة نجد أن B1 ,B2 بين السلكين في اتجاه واحد فتنشأ قوة تنافر بينهما
إيجاد بعد نقطة التعادل
نقطة التعادل : هي النقطة التي تنعدم عندها محصلة المجالين المغناطيسي وتكون عندها محصلة المجالين =0 ودائماً أقرب ما يكون للسلك الذي يمر به تيار شدته أقل
المجال المغناطيسي الناتج عن أربعة أسلاك
أربعة أسلاك يحمل كل منها تياراً مقداره 1A وتوجد الأسلاك في الزوايا الأربع لمربع كول ضلعه a=3.7cm ويحمل سلكان منهما التيار إلى داخل الصفحة بينما يحمل الاثنان الأخران التيار خارج الصفحة ما مركبة المجال المغناطيسي العمودية BY في مركز المربع
القوة المغناطيسية المبذولة على حلقة يمر بها تيار كهربائي
يحمل سلك طويل مستقيم تياراً مقداره i1=5A باتجاه اليمين وتوضع حلقة مربعة يبلغ طول ضلعها a=0.25m بحيث يكون اضلاعها كما في الشكل والمسافة d=0.1 m من السلك وتحمل الحلقة المربعة تياراً مقداره i2=2.2A يعكس اتجاه عقارب الساعة ما محصلة القوى المغناطيسي المؤثرة في الحلقة المربعة
شكل المجال : عند مركز الملف يكاد يكون منتظم وخارجه ( غير منتظم ) على شكل منحنيات مغلقة يشبه المجال المغناطيسي الناشئ عن قضيب مغناطيسي قصير
قانون أمبير
استخدامه :
يستخدم لحساب المجال المغناطيسي الناتج عن توزيع عناصر التيار عندما يكون للتوزيع تماثل أسطواني أو غير ذلك من أنواع التماثل
المجالات المغناطيسية الخاصة بالملفات اللولبية والحلقية
ملف هلمهولتز
يتكون من حلقتين محوريتين من السلك بحيث كل حلقة تتكون من حلقات متعددة او من لفات من سلك واحد
ينشأ عنه مجالات مغناطيسية منتظمة داخل الملف بين الحلقات ومجال غير منتظم خارج الملف
الملف اللولبي ( الحلزوني )
وصف المجال المغناطيسي الناشئ عن مرور تيار في ملف لولبي
شكل المجال :عند محورالملف يكاد يكون منتظم وخارجه ( غير منتظم ) على شكل منحنيات مغلقة يشبه المجال المغناطيسي الناشئ عن قضيب مغناطيسي طويل
الملف الحلقي ( المغناطيس الحلقي )
هو ملف لولبي ثني بحيث يلتقي طرفاه معاً ( على شكل الدائرة ) ويعطي المجال المغناطيسي داخله
تحديد اتجاه المجال المغناطيسي للملف الحلقي
نستخدم قاعدة اليد اليمنى الرابعة الموضحة بالشكل المقابل
إيجاد عدد اللفات للملف احلقي N
من خلال قسمة طول السلك L على محيط المقطع العرضي
الذرات كمغناطيسيات
تحتوي الذرات التي تتكون منها كل مادة على الكترونات متحركة حيث تكون الالكترونات حلقات تيار وتنتج مجالاً مغناطيسياً
فإذا كانت حلقات التيار
موجهة بشكل عشوائي ستكون محصلة المجال المغناطيسي =0
بمحاذاة بعضهما البعض سيكون لها محصلة مجال مغناطيسي وتسمى بالمواد المغناطيسية
أي أن هناك نوعان من العزم المغناطيسي الذري
عزم مغناطيسي مداري : تنشأ عند دوران الالكترون حول النواة
عزم مغناطيسي مغزلي : تنشأ عند دوران الالكترون حول نفسه
أولاً العزم المغناطيسي المداري :
يوضح الشكل المقابل نموذجاً مبسطاً للذرة : الكترون يتحرك بسرعة ثابته في مدار دائري نصف قطره r وبالتالي يمكن اعتابر شحنة الالكترون المتحركة تيار i
شدة التيار : هو مقدار الشحنة التي تمر بنقطة معينة خلال وحدة الزمن
يمكن الحصول على مقدار عزم القطب المغناطيسي لألكترون متحرك بمدار حول النواة
يمكن الحصول على مقدار كمية الحركة الزواية المدارية للالكترون
ثانياً : عزم مغناطيسي مغزلي ( اللف المغزلي )
لا يعد عزم ثنائي القطب المغناطيسي الناتج عن الحركة المدارية للالكترونات المساهم الوحيد في العزم المغناطيسي للذرات حيث أن هناك جسيمات اولية اخرى لها عزم مغناطيسي مثل البروتونات والنيترونات
تحدد الخاصية المغناطيسية لمعظم المادة بالعزوم المغناطيسية للف المغزلي اللألكترون
كما يربط العزم المغناطيسي لجسيم يتمتع بخاصية اللف المغزلي بكمية الحركة الزاوية للف المغزلي للجسيم S
الخواص المغناطيسية للمادة
المغنطة (M )
هي محصلة عزم ثنائي القطب الناتج عن عزوم ثنائيات أقطاب الذرات لكل وحدة حجم من المادة
ملحوظة يعتمد المجال المغناطيسي B داخل المادة على المجال المغناطيسي الخارجي والمغنطة
حيث تحدث المغنطة عند تعرض المادة لمجال مغناطيسي خارجي
المواد الدايامغناطيسية والبارامغناطيسية
تنقسم المواد من حيث مغنطتها إلى ثلاث أقسام :
ديا مغناطيسية بارامغناطيسية فرومغناطيسية
مقارنة بين المواد الديا مغناطيسية والبارامغناطيسية
| وجه المقارنة | المواد الديا مغناطيسية | المواد لبارامغناطيسية |
| غياب مجال مغناطيسي خارجي | ثنائيات القطب تكون مرتبة عشوائياً ومحصلة المجال المغناطيسي داخلها =0 | ثنائيات القطب تكون مرتبة عشوائياً ومحصلة المجال المغناطيسي داخلها =0 |
| وضعها في مجال مغناطيسي خارجي | ثنائيات القطب ترتب نفسها عكس المجال الخارجي كما يستحث فيها مجال معاكس للمجال الخارجي | ثنائيات القطب ترتب نفسها باتجاه المجال الخارجي كما يستحث فيها مجال معاكس للمجال الخارجي |
| المغنطة M | صغيرة ومعاكسة لاتجاه المجال الخارجي H | صغيرة وبنفس اتجاه المجال الخارجي H |
| القابلية المغناطيسية | Xm<0سالبة | Xm>0 موجبة |
| المغنطة ودرجة الحرارة | المغنطة لا تعتمد على الحرارة | |
| إزالة المجال الخارجي | تزول المغنطة | تزول المغنطة |
| وضعها في مجال خارجي غير منتظم | تتأثرة بقوة اتجاه منطقة المجال الأقل وتتنافر مع المغناطيس المؤثر عليها | تتأثرة بقوة اتجاه منطقة المجال الأكبر وتنجذب مع المغناطيس المؤثر عليها |