حل درس مساحة متوازي الأضلاع والمثلث الرياضيات الصف التاسع
1 التركيز
الهدف إنشاء منصفات عمودية ومنصفات زوايا في المثلثات.
المواد الخاصة لكل مجموعة
فرجار مسطرة تقويم
نصيحة للتدريس
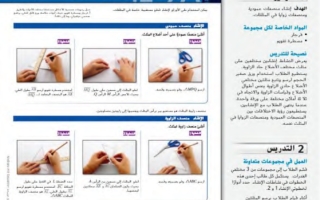
يعرض النشاط إنشاءين مختلفين على مثلث مختلف الأضلاع حاد الزاوية.
يستطيع الطلاب استخدام ورق صغير الحجم لرسم وتتبع مثلثين مختلفين الأضلاع احادي الزاوية بنفس أطوال الأضلاع وقياسات الزاوية والاتجاه في ثلاثة أماكن مختلفة على ورقة واحدة.
تابع مع الإنشاءين. يستطيعون رؤية الاختلافات بين
المنصفات العمودية ومنصفات الزوايا في المثلث نفسه.
2 التدريس
العمل في مجموعات متعاونة
قسم الطلاب إلى مجموعات من 3 مختلفي القدرات. يستكمل كل طالب إحدى هذه الخطوات في نشاطات الإنشاء حدد أدوارا لخطوتي الإنشاء 1 و 2. أثناء قيام الطلاب برسم المثلثين المتطابقين لإثبات التنصيف العمودي
في النشاط رقم 1. أخبرهم أن بإمكانهم استخدام النقطة P أو النقطة Q لأن كلتا مجموعتي الأقواس تم رسمهما بنفس فتحة المرجار.
تمرين اجعل الطلاب يستكملوا التمرين t أثناء، إجراء النشاطات.
الهدف إنشاء وسيطات وارتفاعات
المواد الخاصة لكل مجموعة
• فرجار مسطرة تقويم
نصيحة للتدريس
عرض النشاط إنشاءين مختلفين على مثلث مختلف الأضلاع حاد الزاوية.
يستطيع الطلاب استخدام ورق صغير الحجم لرسم وتتبع مثلثين مختلفي الأضلاع احادي الزاوية بنفس أطوال الأضلاع وقياسات الزاوية والاتجاه في ثلاثة أماكن مختلفة على ورقة واحدة عندما ينتهي الطلاب مع الإنشاءين. يستطيعون رؤية الاختلافات بين الوسيطات والارتفاعات في المثلث نفسه.
2 التدريس
العمل في مجموعات متعاونة
قسم الطلاب إلى مجموعات من ثلاثة مختلفي القدرات ينتقي كل طالب إحدى هذه الخطوات في نشاطات الإنشاء. حدد أدوارا لخطوتي الإنشاء ١ و2.
تمرين أطلب من الطلاب إتمام التمرين ١ و2
3 التقويم
التقويم التكويني
استخدم التمرينين 1 و 2 لتقويم ما إذا كان الطلاب يستوعبون إنشاء الوسيطات والارتفاعات.
2 التدريس
العمل بصورة مستقلة
يستطيع الطلاب العمل بمفردهم أو في مجموعات ثنائية من الطلاب مختلفي القدرات. اطلب من الطلاب أن ينفذوا النشاط أثناء الإجابة على التمارين من ا إلى 6.
اسأل الطلاب عن الرابط بين تخمينهم في التمرين 4 وما لاحظوه اجعل الطلاب يحددوا كيفية النقر على الرأس A وسحبه يقع على أقصر مسافة من الرأس 8.
تمرين اطلب من الطلاب إتمام التمرين 7 بمفرده
3 التقويم
التقويم التكويني
استخدم التمارين من 1 إلى 7 لتقويم ما إذا كان الطلاب يفهمون العلاقات أطوال أضلاع المثلثات.
من العملي إلى النظري
اجعل الطلاب يرسموا مثلثا على ورقة رسوم بيانية. اطلب منهم أن يتبادلوا مثلثاتهم مع زملائهم أجعل الطلاب يتوصلوا إلى أطوال الأضلاع ويمكنوا المتباينات للتعبير عن العلاقات بين الأطوال.
قبل الدرس 12-9 كتابة البراهين الإحداثية.
الدرس 12-9 حساب محيط ومساحة متوازيات الأضلاع والمثلثات.
الدرس 12-9 التعرف على خواص متوازيات الأضلاع وتطبيقها.
2 التدريس
الأسئلة الداعمة
اطلب من الطلاب قراءة القسم لماذا؟ الوارد في هذا الدرس.
اطرح الأسئلة التالية:
• ما الأشكال التي يمكن عمليا من هذا اللغز ؟ الإجابة النموذجية، أرنب، قطة وبطة.
وضح السبب وراء تطابق مساحات الشكل الثاني والشكل الرابع. لأن مساحة القطع التي تشكل كلا منهما متشابهة.
• ما الطريقة السهلة التي يمكن من خلالها حساب مساحة أحد تلك الأشكال ؟ الإجابة النموذجية. من خلال حساب مساحة المربع.
التدريس باستخدام التكنولوجيا
اللوحة البيضاء التفاعلية
اعرض متوازي أضلاع على اللوحة وارسم قطرا من أقطاره. تتبع متوازي الأضلاع لترسم مثلثين. اسحبهما بعيدا وأرجعهما معا لتوصف للطلاب أن مساحة متوازي الأضلاع عبارة عن مجموع مساحتي هذين المثلثين مساحات المثات
يوضح المثالان 3 4 g كيفية استخدام مساحات المثلثات في حساب القيم المجهولة.
مثال إضافي
صندوق الرمال ستحتاج إلى شراء ما ينبغي من اللوحات لتصنع إطارا لصندوق الرمال المثلث الموضح وما يكفي من الرمال لملئه. إذا كانت اللوحة الواحدة طولها 3 أمتار وحقيبة الرمال الواحدة تملأ 9 أمتار مربعة من صندوق الرمال، فكم عدد اللوحات والحقائب التي سوف تحتاج إلى شرائها ؟ 12 لوحة و 6 حقائب
إرشاد للمعلمين الجدد
الاستنتاج المنطقي تستطيع أن تجعل الطلاب يكونوا أشكالا عدة على ورق التمثيل البياني ليتحققوا من معادلات حساب المساحات لمتوازيات الأضلاع والمثلثات.
الجبر ارتفاع المثلث يزيد يمقدار سنتيمترات عن قاعدته. مساحة المثلث تبلغ 60 سنتيمترا مربعا.
احسب القاعدة والارتفاع.
التركيز على محتوى الرياضيات
وضح أنه من الممكن أن يتم رسم العديد من مختلف متوازيات الأضلاع بالارتفاع نفسه ومع كون قواعدها متطابقة، ومن ثم بالمساحة نفسها. استخدم لوحة جغرافية أو جهاز تصميم مماثلا لتوضح مختلف منوازيات الأضلاع التي لها نفس الطول والقاعدة.
اطلب من الطلاب أن يوضحوا مدى اختلاف متوازيات الأضلاع تلك.
إرشاد للمعلمين الجدد
تمثيل النماذج ساعد الطلاب على فهم العلاقة بين مساحة المثلث ومساحة متوازي الأضلاع أو المستطيل من خلال عرض نموذج أمامهم. اقطع قطعة من الورق حجمها 21 سنتيمترا 27.5 سنتيمترا نصفين على امتداد القطر لنوضح أن مساحة المثلث تبلغ نصف مساحة المستطيل الذي له نفس القاعدة والارتفاع. ثم اقطع مثلثا قائم الزاوية من طرف ورقه أخرى حجمها 21 سنتيمترا 27S سنتيمترا بحيث يكون لها نفس ارتفاع الورقة الأصلية.
شكل متوازي أضلاع من الورقة عن طريق وضعها على الطرف الآخر من الورقة. ثم افطعها نصفين على امتداد القطر. مساحة المثلث تبلغ نصف مساحة متوازي الأضلاع المناظر هذا.
4 التقويم
عين مصطلح الرياضيات
اجعل الطلاب يشرحوا كيفية حساب مساحة المثلث
36d. الإجابة النموذجية: تزيد المساحة بزيادة الطول من 1 إلى 3. وتكون في اعلى قيمة عند 3. ثم تتناقص بزيادة الطول إلى 5
64e. الإجابة النموذجية، يصل التمثيل البياتي لأعلى نقطه عندما 3. ومن ثم ستكون مساحة المستطيل الأكبر عندما يكون الطول 2 ويصل التمثيل البياني لأصغر نقاطه عندما ومن ثم ستكون مساحة المستطيل الأصغر عندما يكون الطول 1 أو 5
E وحدة: الإجابة النموذجية. رسمت المثلث داخل مربغ 6 في 6 وحسب مساحة المربع وطرحت مساحات المثلثات الثلاثة فإن الزاوية الموجودة داخل المربع والتي تم وضعها حول المثلث المعطى. ومساحة المثلث المعطى هو الفرق، أو 15 وحدة.
اجابات اضافية
46. العينة، عينة منتظمة من 250 ضيفا: المجتمع الإحصائي: كل الصيوف: إحصاء العينة، المبلغ المالي الوسيط المتفق على الوجبات الخفيفة من قبل الضيوف ضمن العبنة؛ معلمة المجتمع الإحصائي: المبلغ المالي الوسيط المتفق على الوجبات الخفيفة من قبل كل الضيوف
47، العينة، عينة عشوائية من 1OO طالب في الصف الثالث الثانوي: المجتمع الإحصائي: جميع طلاب الصف الثالث الثانوي في مدرسة البراء بن عازب الثانوية: إحصاء العينة: متوسط المبلغ المالي المتفق على حفل التجرج: معلمة المجتمع الإحصائي: متوسط المبلغ المالي الذي ينفقه طلاب الصف الثالث الثانوي في مدرسة البراء بن عازب الثانوية على حفل التخرج
الهدف فهم ما تتكون منه الأنشطة ذات الإجابات القصيرة وتطوير أساليب لحلها.
2 التدريس
الأسئلة الداعمة
اطرح الأسئلة التالية:
اذكر بعض الطرق التي يختلف فيها حل الأسئلة ذات الإجابات القصيرة عن حل أنشطة الاختبار من متعدد. وما أوجه الشبه بينهما؟ الإجابة النمودجية. يجب أن نكتب الحل في الأسئلة ذات الإجابات القصيرة. وهذا ليس ضروريا في أنشطة الاختيار من متعدد تحسب الأسئلة ذات الإجابات القصيرة باستخدام معايير رصد الدرجات، وبالتالي يمكن منح جزء من الدرجة. أما في أسئله الاختيار من متعدد فالإجابة إما صحيحة أو خطأ وكلا النوعين من الأسئلة يحتاج إلى القراءة المتأنية.
• ما أهمية شرح التبرير في الأسئلة ذات الإجابات القصيرة ؟ الإجابة النموذجية: لا تمنح الدرجة كاملة إلا على الإجابات الصحيحة المدعومة بالشرح الوافي
• ما أهمية التحقق من الإجابة ؟ الإجابة النموذجية، ستؤدي أخطاء السيو إلى الحصول على جزء من الدرجة أو عدم الحصول عليها.
الإجابة النموذجية: كان ينبغي أن يكون التذبذب مرتفعا ويتناقص سريعا من أجل تشكيل مثلث منفرج الزاوية.
57-. مطلقا: جميع المثلثات متساوية الزوايا لها زوايا بمقياس 600. إذا فهي ليس بها زاوية بقياس "90. وبالتالي لا يمكن أن تكون مثلث قائمة الزوايا.
S8 دائما: جميع المثلثات متساوية الأضلاع لها ثلاثة أضلاع متساوية والمثلثات متساوية الساقين لها على الأقل ضلعان متساويان، إذا جميع المثلثات التي لها ثلاثة أضلاع متساوية فهي متساوية الساقين.
59. مطلقا: جميع المثلثات متساوية الأضلاع متساوية الزوايا أيضا. مما يعني أن جميع الزوايا تساوي 600. المثلث قائم الزاوية له زاوية واحدة بمقياس 900.
60. الإجابة النودجية: بما أن المثلث متساوي الأضلاع فإن جميع الأضلاع متساوية. وبجعل 3+5X تساوي 5— 7x وإيجاد الحل. فإن ا ساوي 4. طول الضلع الواحد يساوي 3 (4)5 أو 23 وحدة. محيط المثلث متساوي الأضلاع يساوي مجموع أضلاعه الثلاثه أو ضرب الضلع في ثلاثة. المحيط يساوي (23)3 أو 69 وحدة.