حل درس المثلثات والبرهان الأحداثي الرياضيات الصف التاسع
1 التركيز
التخطيط الرأسي
قبل الدرس 12 -8 استخدام هندسة الإحداثيات لإثبات تطابق المثلثات.
الدرس 12-8 نحديد موضع المثلثات وتسميتها لاستخدامها في البراهين الإحداثية. كتابة البراهين الإحدائية.
بعد الدرس 12-8 حساب محيط ومساحة متوازيات الأضلاع والمثلثات.
2 التدريس
الأسئلة الداعمة
اطلب من الطلاب قراءة القسم لماذا الوارد في هذا الدرس.
اطرح الأسئلة التالية:
• ما وجه التشابه بين النظام الإحداثي الذي يستخدمه نظام تحديد المواقع العالمي والنظام الإحداثي الهندسي ؟ المحور x هو خط العرض والمحور y هو خط الطول
• كيف تظن أن القمر الصناعي يحدد موقعك على الأرض ؟ تقبل جميع الإجابات المنطقية.
• ما الذي تريد معرفته لإيجاد المسافة بين نقطتين على المستوى الإحداثي ؟ ينبغي معرفة الإحداثيات لكل نقطة.
التدريس باستخدام التكنولوجيا
اللوحة البيضاء التفاعلية اعرض مثلثا على اللوحة ولرسم مستوى إحداثيا بحيث يتم وضع واحدة من نقاط التقاطع عند النقاط (b a) في الربع الأول. ثم أعد رسم المستوى الإحداثي بحيث نضع نقطة التقاطع عند النقطة (0 0). وضح لطلابك أن ذلك من شأنه أن يساعد في تبسيط العمليات الحسابية.
ارشاد للمعلمين الجدد
التبرير بما أن البراهين الإحداثية تجمع بين الهندسة والجبر ذكر الطلاب بأنهم سيحتاجون إلى استخدام قوانين المسافة والميل ونقطة المنتصف. وكذلك المسلمات والنطريات. انصح الطلاب بالبحث عن المفردات الأساسية مثل "الطول" أو "التوازي" في المسائل الكلامية. مما قد يشير إلى إمكانية استخدام قانون معين لحل المسألة.
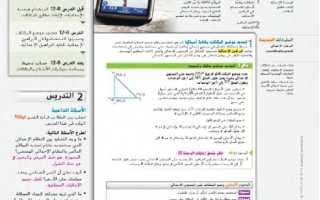
مثال إضافي الرسم اكتب برهانا إحداثيا لإثبات أن أداة الرسام هذه تطبق المثلث قائم الزاوية. طول أحد الأضلاع يساوي 25 سنتيمترا وطول الضلع الآخر يساوي 145 سنتيمترا.
1 تحديد مواضع المثلثات وتسميتها
يوضح المثالان 1و 2 كيفية استخدام البراهين الإحداثية لإثبات المفاهيم الهندسية.
التقويم التكويني
استخدم التمارين الواردة في القسم "تمرين موجه" بعد كل مثال للوقوف على مدى استيعاب الطلاب للمفاهيم
أمثلة إضافية
حدد موضع واسم المثلث قائم الزاوية XYZ على أن يبلغ طول الساق من الوحدات على المستوى الإحداثي.
عين الإحداثيات المجهولة للمثلث متساوي الساقين القائم الزاوية
2 كتابة البراهين الإحداثية
يوضح المثالان 3 و 4 للطلاب كيفية استخدام الخواص و النظريات في كتابة البراهين الإحداثية.
مثال إضافي
اكتب البرهان الإحداثي لإثبات أن القطعة المستقيمة التي تصل بين زاوية الرأس في المثلث متساوى الساقين و نقطة منتصف قاعدته متعامدة على القاعدة.
التدريس المتمايز
النمط البصري / المكاني زود الطلاب بنسخة خريطة شفافة. واطلب من الطلاب اختيار ثلاث وجهات و استخدام تلك الرؤوس لرسم مثلث. بعد ذلك، يضع الطلاب الخريطة الشفافة على المستوى الإحداثي شجع الطلاب على التجرية باستخدام هذا الموضع. و في النهاية اطلب من الطلاب أستخدام البرهان الإحداثي لنصفي المثلث.
4 التقويم
عين مصطلح الرياضيات اطلب من الطلاب ذكر كيف يمكنهم تحديد موضع أشكال معينة في المستوى الإحداثي أسماء الرؤوس. و قد يناقش و كيف يحددون الطلاب أفكارا متنوعة حول تحديد الموضع و حول كيفية تبسيط البراهين الإحدائية عن طريق استخدام الأساليب الأصلية والبسيطة في تحديد الأسماء.